[ROT13 at Warp Speed: A Practical Optimization Playbook]
Analyze with AI
Get AI-powered insights from this Mad Devs tech article:
Intro
Sometimes we do optimizations just for fun (see previous write-up). This one was also done for fun, but the methods described below are used in real projects, I swear. 😀
Problem statement
ROT13 is a simple letter substitution cipher that replaces a letter with the letter 13 letters after it in the alphabet. ROT13 is an example of the Caesar cipher. Create a function that takes a string and returns the string ciphered with ROT13. If numbers or special characters are included in the string, they should be returned as they are. Only letters from the Latin/English alphabet should be shifted, like in the original ROT13 "implementation."
That sounds quite easy and can be done in 3 minutes during the interview, right? Right. So the first implementation was:
std::string rot13_naive(const std::string &input) {
std::string result = input;
for (char &c : result) {
if (c >= 'a' && c <= 'z') {
c = (c - 'a' + 13) % 26 + 'a';
} else if (c >= 'A' && c <= 'Z') {
c = (c - 'A' + 13) % 26 + 'A';
}
}
return result;
}1st optimization: Remove branches and divisions/mods
First of all, instead of processing uppercase and lowercase characters separately, we want to calculate the "offset" and add it to the original character. The default value for the offset is 0. If the character is alpha – set the offset to 13. If the character is greater than ('z' - 13) – set offset to -13.
Second, we don't want division and mod operations. We need to replace % 26 with constant adds/subs.
The first step is to convert the character to lower case (it can be done by | 0x20). After that, we want to check if the character is in range ['a'..'z']. And finally, we want to adjust the offset by comparing it with 'm' ('z' - 13). Here is the listing:
char rot13(char c) {
char cl = c | 0x20; // to lower
int8_t is_alpha = (uint8_t)(cl - 'a') <= 'z' - 'a';
int8_t offset = 13 - 26 * (cl > 'm');
c += is_alpha * offset;
return c;
}This version, obviously, should work faster, right? Wrong, it does not 🙂 Actually, it depends on the input. The first version returns immediately after the range check if the character is not alpha. The second version always applies all operations.

BUT! This code is much simpler for the next optimizations (see below).
2nd optimization: Lookup table
This is the second obvious optimization. Just precalculate all possible values for all possible inputs, place them in an array, and get instant access to the result character.
alignas(64) static unsigned char lut[256];
struct lut_init {
lut_init() {
for (int i = 0; i < 256; ++i) {
unsigned char c = i, cl = c | 0x20;
bool a = (cl >= 'a' && cl <= 'z');
bool m = (cl > 'm');
lut[i] = a ? (unsigned char)(c + 13 - (m ? 26 : 0)) : c;
}
}
} lut_init__;
void rot13_lut(char *str, size_t n) {
for (size_t i = 0; i < n; ++i)
str[i] = lut[(uint8_t)str[i]];
}This one works faster than most methods below (but not the fastest, though).
3rd optimization: Process many bytes per instruction (SIMD)
The branchless version seems super simple and can be implemented with SIMD instructions. We need to define some masks to make this simple arithmetic work.
Key steps per 16-byte block:
lower_case = bytes | 0x20is_alpha = (lower_case >= 'a') & (lower_case <= 'z')greater_than_m = (lower_case > 'm')within alphabetoffset = 13only whereis_alphamsk26 = 26only whereis_alpha & greater_than_morig += offset; orig -= msk26- store back
The implementation looks like this:
void rot13_sse(char *str, size_t n) {
const __m128i msk_20 = _mm_set1_epi8(0x20);
const __m128i msk_a = _mm_set1_epi8('a');
const __m128i msk_m = _mm_set1_epi8('m' + 1);
const __m128i msk_z = _mm_set1_epi8('z' + 1);
const __m128i msk_13 = _mm_set1_epi8(13);
const __m128i msk_26 = _mm_set1_epi8(26);
const __m128i msk_00 = _mm_setzero_si128();
const __m128i msk_ff = _mm_cmpeq_epi8(msk_00, msk_00);
uintptr_t p_str = (uintptr_t)str;
uintptr_t p_aligned = (p_str + 15) & ~((uintptr_t)15);
// for unaligned data we use naive approach
char *s = str;
size_t i = 0;
for (; s != (char *)p_aligned && i < n; ++s, ++i) {
*s = rot13(*s);
}
auto transform16 = [&](__m128i v) -> __m128i {
__m128i lower_case = _mm_or_si128(v, msk_20);
__m128i gt_a = _mm_cmpgt_epi8(msk_a, lower_case);
gt_a = _mm_xor_si128(gt_a, msk_ff);
__m128i le_z = _mm_cmpgt_epi8(msk_z, lower_case);
__m128i is_alpha = _mm_and_si128(gt_a, le_z);
__m128i lower_alphas = _mm_and_si128(is_alpha, lower_case);
__m128i gt_m = _mm_cmpgt_epi8(msk_m, lower_alphas);
gt_m = _mm_xor_si128(gt_m, msk_ff);
gt_m = _mm_and_si128(gt_m, is_alpha);
__m128i off_1 = _mm_and_si128(msk_13, is_alpha);
__m128i off_2 = _mm_and_si128(msk_26, gt_m);
v = _mm_add_epi8(v, off_1);
v = _mm_sub_epi8(v, off_2);
return v;
};
// sse while possible
for (; i + 16 <= n; s += 16, i += 16) {
__m128i orig = _mm_load_si128((__m128i *)s);
orig = transform16(orig);
_mm_store_si128((__m128i *)s, orig);
}
for (; *s && i < n; ++s, ++i) {
*s = rot13(*s);
}
}This looks much harder to implement, but it works noticeably faster than LUT.
4th optimization: Launch in parallel on different CPU cores
The next obvious optimization is to run the whole process on several CPU cores. We split the buffer into per-core chunks and pin threads using the set affinity function.
Here is the pattern I use on Linux machines. Be careful – std::thread::hardware_concurrency (which I used at the beginning) is not a reliable method to get the number of available CPU cores. Instead, use something more platform-dependent. On Linux, it's possible to acquire online available CPUs by get_nprocs(). On Windows, there is a function GetSystemInfo which can return a SYSTEM_INFO structure containing the field dwNumberOfProcessors.
void run_in_parallel(std::function<void(size_t)> pf_func) {
size_t cpu_n = get_cpu_count();
std::vector<std::thread> threads(cpu_n);
for (size_t i = 0; i < cpu_n; ++i) {
threads[i] = std::thread([pf_func, i]() { pf_func(i); });
cpu_set_t cpuset;
CPU_ZERO(&cpuset);
CPU_SET(i, &cpuset);
int rc = pthread_setaffinity_np(threads[i].native_handle(),
sizeof(cpu_set_t), &cpuset);
if (rc != 0) {
std::cerr << "Error calling pthread_setaffinity_np: " << rc << "\n";
}
}
for (auto &t : threads) {
if (!t.joinable())
continue;
t.join();
}
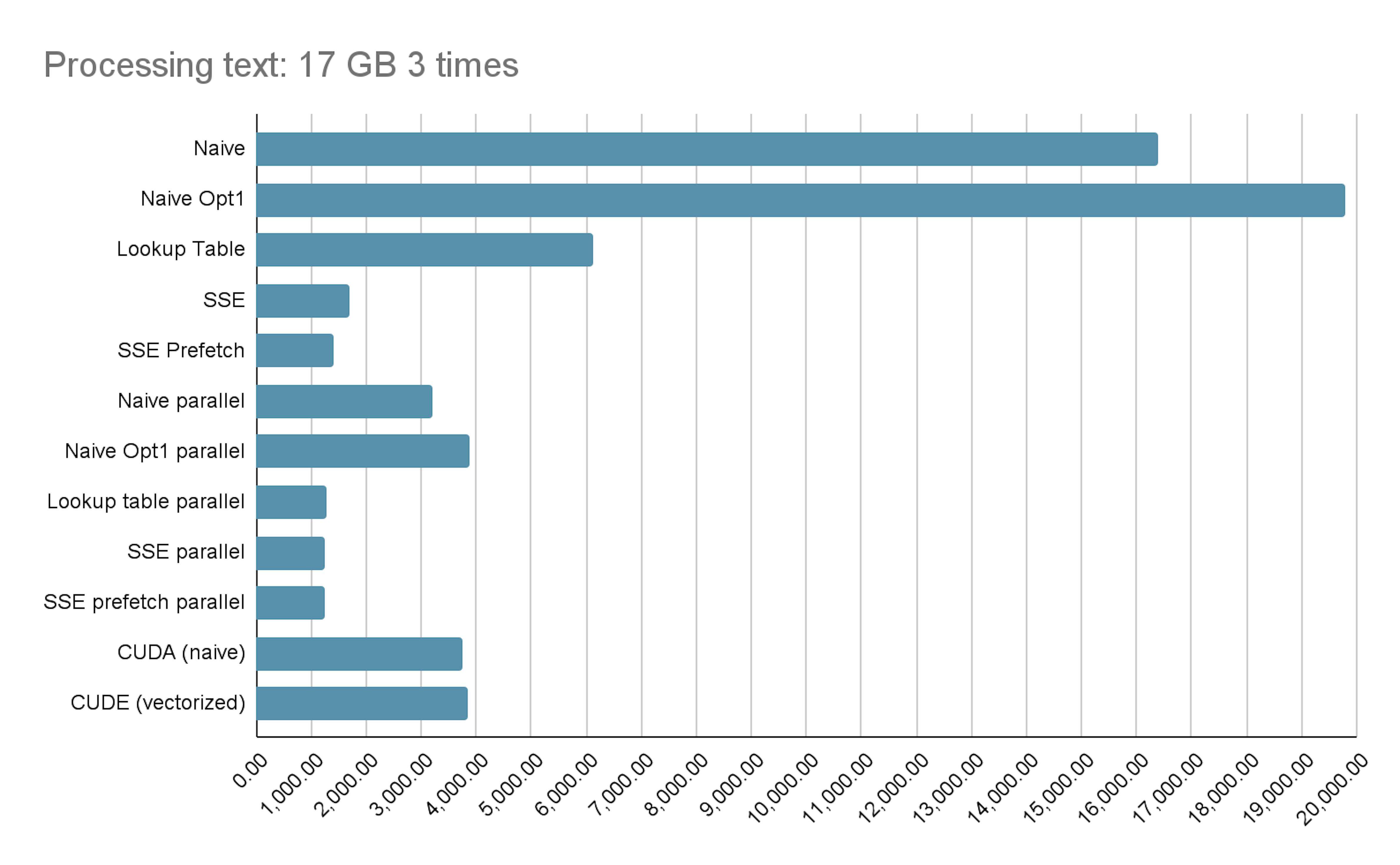
}We can launch every previous method in parallel to compare them with each other and the single-threaded version. Here are the results:
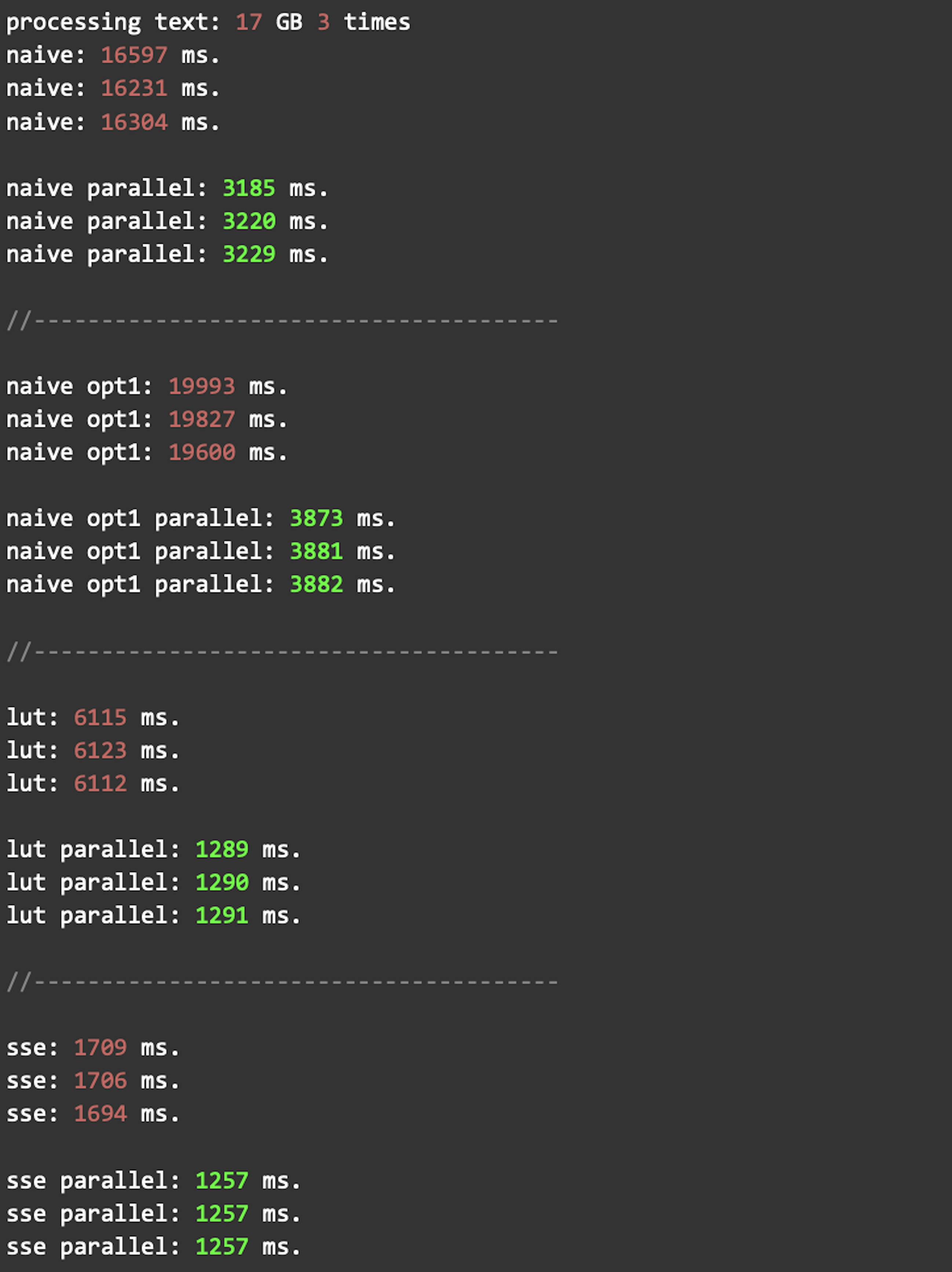
5th optimization: Cache line-sized unrolled main loop
The last CPU optimization is to make this loop more cache-friendly. SSE has special instructions to prefetch data into cache (L1/L2). To make this optimization, we have to split the buffer into 64B (typical cache line) chunks and manually unroll our SSE loop to process every chunk. This reduces loop overhead and helps the core keep load/compute/store pipeline busy.
void rot13_sse_prefetch(char *str, size_t n) {
const __m128i msk_20 = _mm_set1_epi8(0x20);
const __m128i msk_a = _mm_set1_epi8('a');
const __m128i msk_m = _mm_set1_epi8('m' + 1);
const __m128i msk_z = _mm_set1_epi8('z' + 1);
const __m128i msk_13 = _mm_set1_epi8(13);
const __m128i msk_26 = _mm_set1_epi8(26);
const __m128i msk_00 = _mm_setzero_si128();
const __m128i msk_ff = _mm_cmpeq_epi8(msk_00, msk_00);
uintptr_t p_str = (uintptr_t)str;
uintptr_t p_aligned = (p_str + 15) & ~((uintptr_t)15);
// for unaligned data we use naive approach
char *s = str;
size_t i = 0;
for (; s != (char *)p_aligned && i < n; ++s, ++i) {
*s = rot13(*s);
}
const size_t CACHELINE = 64;
const size_t PF_L1_DIST = 4 * CACHELINE; // prefetch ~256B ahead to L1
const size_t PF_L2_DIST = 12 * CACHELINE; // prefetch ~768B ahead to L2
auto transform16 = [&](__m128i v) -> __m128i {
__m128i lower_case = _mm_or_si128(v, msk_20);
__m128i gt_a = _mm_cmpgt_epi8(msk_a, lower_case);
gt_a = _mm_xor_si128(gt_a, msk_ff);
__m128i le_z = _mm_cmpgt_epi8(msk_z, lower_case);
__m128i is_alpha = _mm_and_si128(gt_a, le_z);
__m128i lower_alphas = _mm_and_si128(is_alpha, lower_case);
__m128i gt_m = _mm_cmpgt_epi8(msk_m, lower_alphas);
gt_m = _mm_xor_si128(gt_m, msk_ff);
gt_m = _mm_and_si128(gt_m, is_alpha);
__m128i off_1 = _mm_and_si128(msk_13, is_alpha);
__m128i off_2 = _mm_and_si128(msk_26, gt_m);
v = _mm_add_epi8(v, off_1);
v = _mm_sub_epi8(v, off_2);
return v;
};
// cacheline while possible
for (; i + CACHELINE <= n; s += CACHELINE, i += CACHELINE) {
if (i + PF_L1_DIST < n)
_mm_prefetch((const char *)(str + i + PF_L1_DIST), _MM_HINT_T0);
if (i + PF_L2_DIST < n)
_mm_prefetch((const char *)(str + i + PF_L2_DIST), _MM_HINT_T1);
__m128i v0 = _mm_load_si128((__m128i *)(s + 0));
__m128i v1 = _mm_load_si128((__m128i *)(s + 16));
__m128i v2 = _mm_load_si128((__m128i *)(s + 32));
__m128i v3 = _mm_load_si128((__m128i *)(s + 48));
v0 = transform16(v0);
v1 = transform16(v1);
v2 = transform16(v2);
v3 = transform16(v3);
_mm_store_si128((__m128i *)(s + 0), v0);
_mm_store_si128((__m128i *)(s + 16), v1);
_mm_store_si128((__m128i *)(s + 32), v2);
_mm_store_si128((__m128i *)(s + 48), v3);
}
// sse while possible
for (; i + 16 <= n; s += 16, i += 16) {
__m128i orig = _mm_load_si128((__m128i *)s);
orig = transform16(orig);
_mm_store_si128((__m128i *)s, orig);
}
for (; *s && i < n; ++s, ++i) {
*s = rot13(*s);
}
}This is the fastest implementation for now:
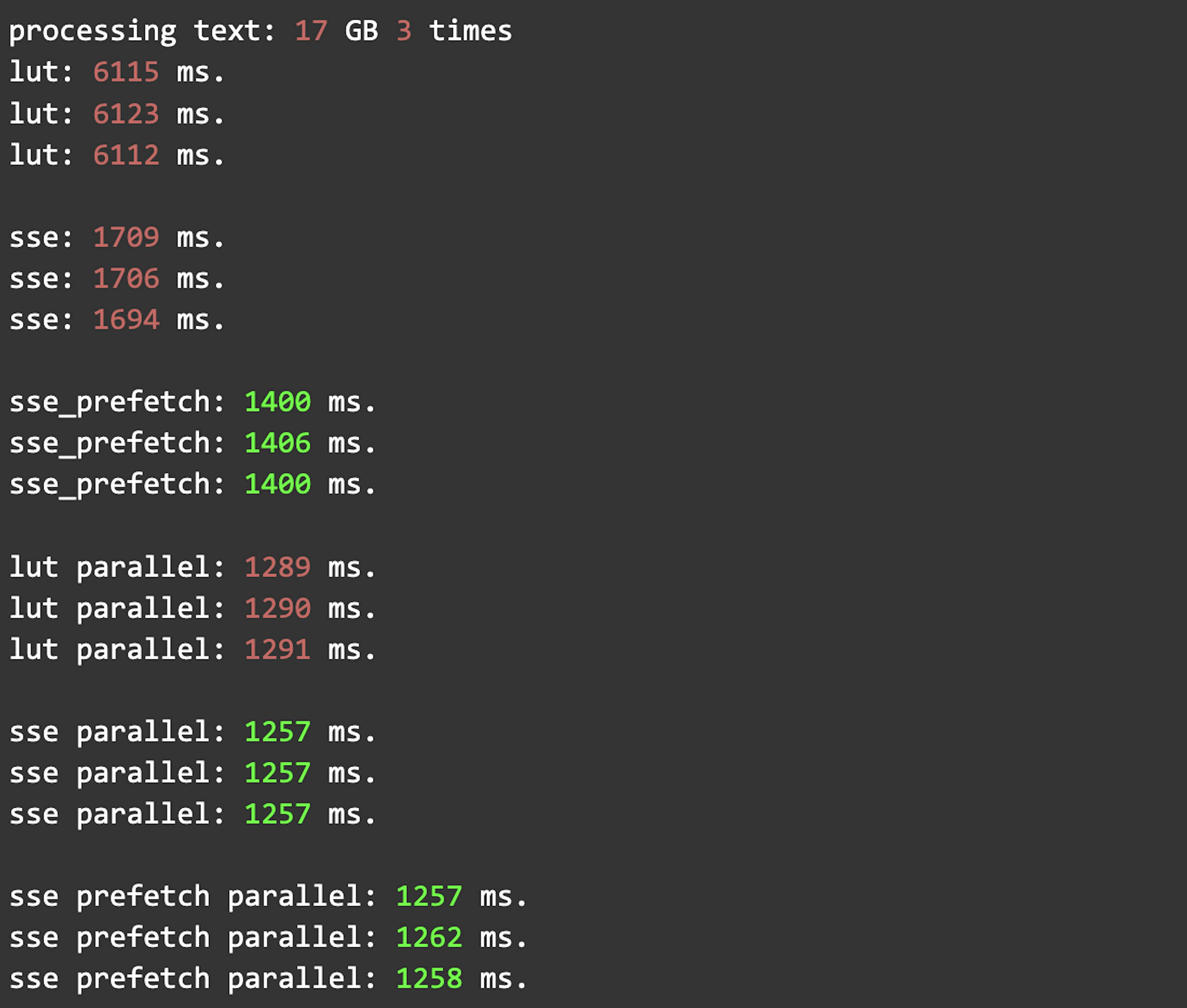
On several CPUs, the SSE version with prefetch works almost as fast as the SSE version without it. But single-threaded SSE with prefetch works faster.
6th optimization: AVX2/AVX512
Unfortunately, I don't have a CPU with AVX512 instructions. But an implementation can be found in the repository. AVX-based methods likely work even faster than SSE methods. At least the AVX512 version seems more straightforward because there are greater equal and less equal functions (SSE does not have them).
7th optimization: CUDA
For now, we have probably the fastest version on the CPU. But there is another computation unit – the GPU. Let's check if it works even faster.
I have a CMake-based project, so it did not take much time to add a CUDA implementation.
To enable it in the project, we need to add these lines to CMakeLists.txt:
# my default host compiler is gcc 15
set(CMAKE_CUDA_HOST_COMPILER g++-14)
set(CMAKE_C_COMPILER gcc-14)
set(CMAKE_CXX_COMPILER g++-14)
project(<projectname> LANGUAGES CXX CUDA)
set(CMAKE_CUDA_STANDARD 20)
set(CMAKE_CUDA_STANDARD_REQUIRED ON)
set(CMAKE_CUDA_ARCHITECTURES "52;60;61;62;70;75;80;86")Also, we need to add our .cuh and .cu files to the sources.
file(GLOB_RECURSE sources src/*.cpp src/*.cu inc/*.h inc/*.cuh)That's it. Now we need to add CUDA-based implementations and benchmark them.
Actually, programming with CUDA is different from the usual one. I will not place the whole implementation here; I'll just place a piece of code to highlight differences.
__device__ __forceinline__ char rot13_char(char c) {
char cl = c | 0x20; // to lower
int8_t is_alpha = (uint8_t)(cl - 'a') <= 'z' - 'a';
int8_t offset = 13 - 26 * (cl > 'm');
c += is_alpha * offset;
return c;
}
__global__ void __cuda_rot13(char *str, size_t n) {
// clang-format off
// gridDim.x contains the size of the grid
// blockIdx.x contains the index of the block with in the grid
// blockDim.x contains the size of thread block (number of threads in the thread block).
// threadIdx.x contains the index of the thread within the block
// clang-format on
size_t idx = blockIdx.x * blockDim.x + threadIdx.x;
if (idx >= n)
return;
str[idx] = rot13_char(str[idx]);
}
//////////////////////////////////////////////////////////////
void cuda_rot13(char *str, size_t n) {
size_t threads_n = 1024; // got from ktulhu
size_t blocks_n = std::max(1ul, (n + threads_n) / threads_n);
char *pd_str = nullptr;
cudaError_t err = cudaMalloc((void **)&pd_str, gpu_buff_size);
assert(err == cudaSuccess);
for (size_t i = 0; i < n; i += gpu_buff_size) {
size_t to_copy = ((i + gpu_buff_size >= n) ? n - i : gpu_buff_size);
err = cudaMemcpy(pd_str, &str[i], sizeof(char) * to_copy,
cudaMemcpyHostToDevice);
assert(err == cudaSuccess);
__cuda_rot13<<<blocks_n, threads_n>>>(pd_str, to_copy);
err = cudaMemcpy(&str[i], pd_str, sizeof(char) * to_copy,
cudaMemcpyDeviceToHost);
assert(err == cudaSuccess);
}
cudaFree((void *)pd_str);
}
//////////////////////////////////////////////////////////////
This seems slow, but we need to remember that most time is spent copying from host to GPU memory and back. Probably, this is just not the best task for the GPU. The task is too simple, and CPU parallelism is fast enough due to better data locality, etc.
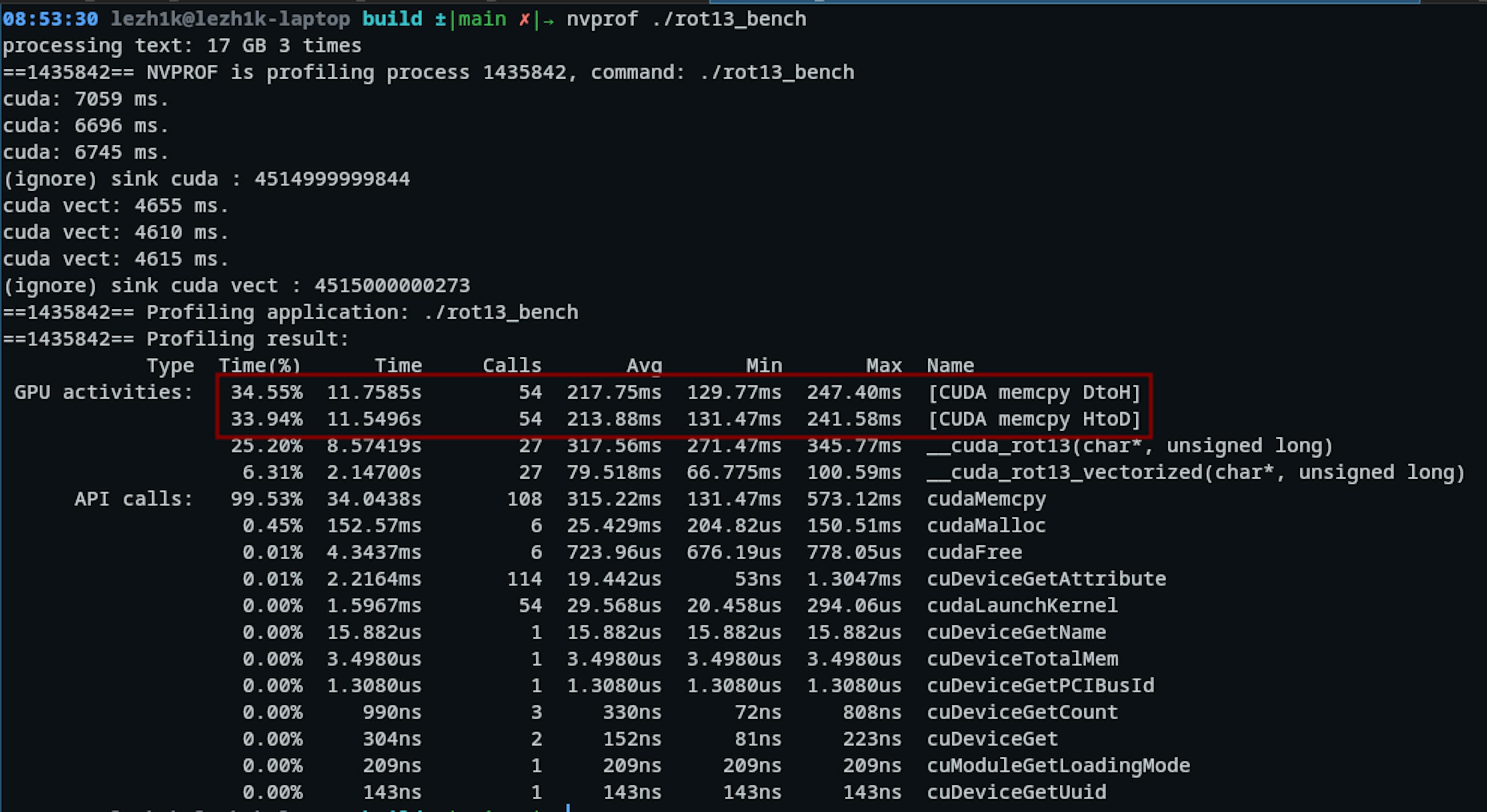
The chart 🙂
Here is a chart with all benchmark results. The champion for now is parallel SSE. If you have an AVX512 instruction, send me profiling results. Source code is available here.