[Write-Up: Santa 2023 - The Polytope Permutation Puzzle / Graph Optimization]
This Kaggle competition is really difficult. We will be very happy to see the winning code. While we haven't had the opportunity to actively participate in the competition, we'd like to share some thoughts on how you can optimize your solution. The approaches I present below won't win you, but with the help of other generative models they can optimize your solution and save you thousands of moves.
The goal of the competition is to complete different puzzles in the minimum number of moves. The organizers provided the initial states and solutions to the puzzles, the allowed moves (replacing elements in the puzzle array using the provided indices gives a new state; but the reverse moves are not given and it seems like a joke) and even gave us solutions (sample submission). I'm guessing that these solutions were generated from the original state by applying random moves and then reversed, so these solutions take over 1.2 million moves in total (the leader at this time reached the solution in just 65,000 moves). And I will describe an approach to optimizing such non-optimized solutions.
How to solve any puzzle?
We can represent any solution as a graph, where each node is a state of the puzzle, and an edge is an applied move. So, if we had unlimited computing resources, we could apply all possible moves to the initial state, then apply all possible moves to each generated state, and after many iterations somewhere we would end up with a solution state and everything we need - is to get the shortest sequence of moves.
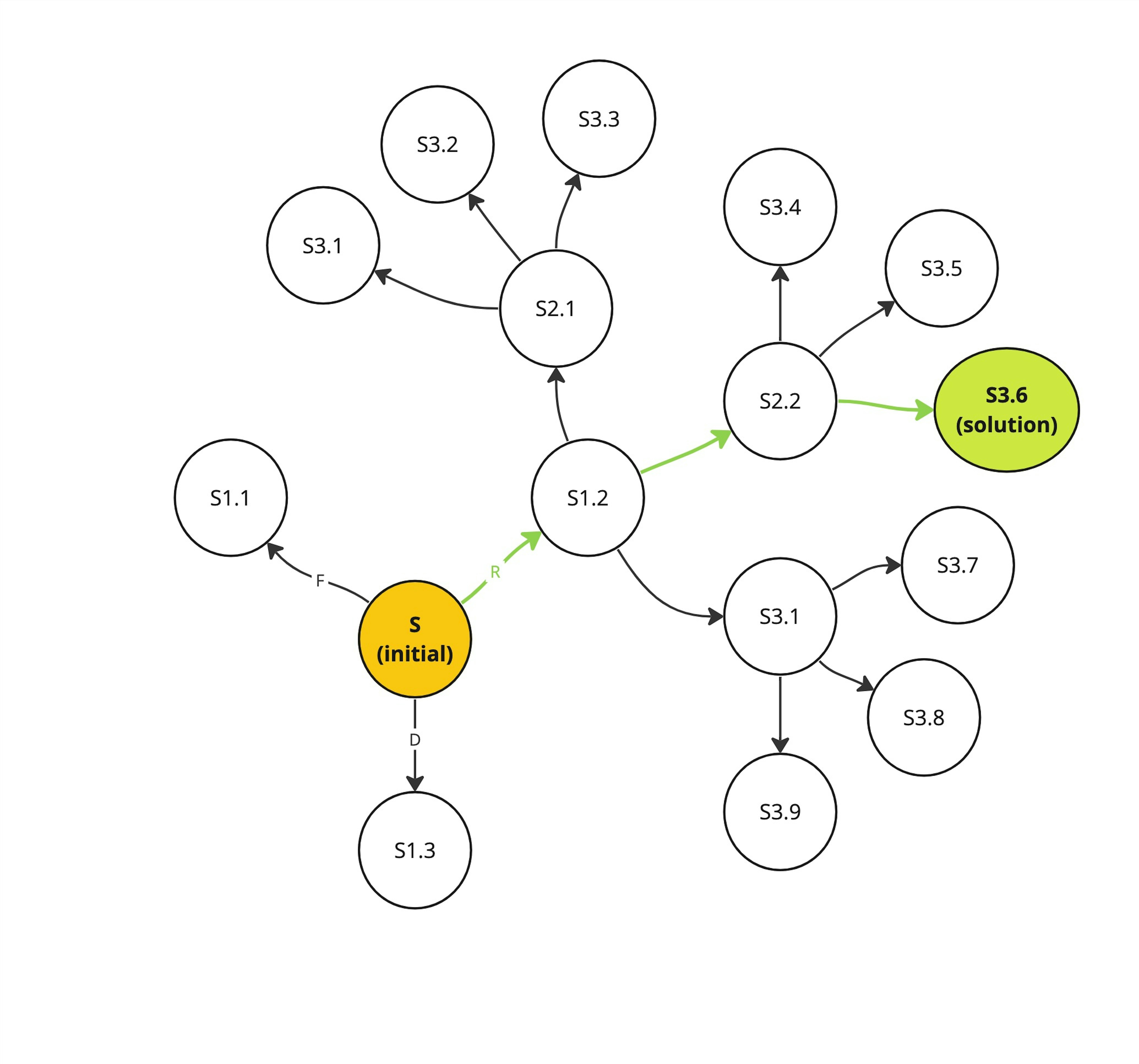
Generation of graph states. To simplify the image, edges for all nodes are not shown. Let's assume that only 3 moves (R, F, D) can be applied to each state; reverse moves are also not shown in the figure.
Obviously, on large puzzles with available computing resources, we can only generate states to a small depth. If we had a good optimization function with which we could select the optimal subsequence, we could reach the solution state iteratively. Perhaps the competition leaders simply came up with such a function.
How to optimize the solution?
But if you generated a sequence of moves using some kind of generative model (for example, as far as I know, there are already NN models for cubes), you can apply graph optimization to your solution anyway you want.
First of all, you can trim the loops in your sequences. In the solutions provided, there were such cycles where we got states that were already there before, and we can simply cut them off. Although this is not a common occurrence.
Loops
Second, we can generate possible states for each state of the sequence (and for each generated state, and then again as long as we have the resources). This will give us a situation where we can reach any of the original states in fewer moves or, in graph terminology, we can find the shortest path.
Finding the shortest path. Instead of 5 moves, using only 3 we can get from S1 to S6
Looks good, but again it doesn't work with large puzzles. If the generated sequence consists of thousands of moves and we have dozens of possible moves, we will very quickly get an out of memory error. Thus, we can apply this approach only to short subsequences of moves and repeat the optimization several times.
No need to remind you that this approach will not lead you to a winner simply by applying it to the solutions provided. I've experimented with some of them. On small puzzles (globe_3/4, 430 moves in a sample submission file), I save about 100 moves with a complete graph construction (without partitioning into subsequences), but on large puzzles (globe_3/33) I could not wait for the calculation, because it could take more than two weeks on my hardware. But obviously you can compute this on the GPU and save a lot of time.
Below I attach the code for such optimization using the NetworkX library. Instead of using the original string states, I used state hashes to save memory. I also attach a handler for globe puzzles because they are the easiest to handle (front rotation is the same in both directions).
from datetime import datetime
import gc
import networkx as nx
from .handlers import GlobeHandler
class GraphOptimizer:
def __init__(
self,
puzzle_type: str,
allowed_moves: str,
depth: int = 3
):
self.handler = GlobeHandler(puzzle_type, allowed_moves)
self.state_hash_dict = {}
self.depth = depth
def optimize(
self,
state: str,
solution_state: str,
moves: list[str],
sub_length: int = 100,
n_epochs: int = 2
) -> list[str]:
# optimize the solutions
moves = self._cut_moves(state, solution_state, moves)
states = self._get_states_by_moves(state, moves)
self.state_hash_dict = {hash(state): state for state in states}
if len(states) < sub_length:
_, moves = self._graph_optimization(states, moves)
for epoch in range(n_epochs):
optim_states, optim_moves = [], []
total = len(states)
for i in range(0, len(states), sub_length):
start = datetime.now()
tmp_states = states[i: i + sub_length]
tmp_moves = moves[i: i + sub_length - 1]
tmp_states, tmp_moves = self._graph_optimization(tmp_states, tmp_moves)
optim_states += tmp_states
optim_moves += tmp_moves
j = i + sub_length - 1
if j < len(moves):
optim_moves += [moves[j]]
print(f'Step {i} / {total}. Time spent: {(datetime.now() - start)}')
gc.collect()
states = optim_states
moves = optim_moves
print(f"Epoch: {epoch}; Sequence len: {len(moves)}")
gc.collect()
gc.collect()
return optim_moves
def _cut_moves(self, state: str, solution_state: str, moves: list[str]) -> list[str]:
# cut off the loops
sequence = []
states = {state: []}
for move in moves:
state = self.handler.apply_move(state, move)
if state == solution_state:
sequence.append(move)
return sequence
if state not in states:
sequence.append(move)
states[state] = sequence.copy()
continue
sequence = states[state]
return sequence
def _get_states_by_moves(self, state: str, moves: list[str]) -> list[str]:
# generate states
states = [state]
for move in moves:
state = self.handler.apply_move(state, move)
states.append(state)
return states
def _graph_optimization(self, states: list[str], moves: list[str]) -> tuple((list[str], list[str])):
# subsequence optimization
if len(moves) == 0:
return states, moves
state, solution_state = states[0], states[-1]
G = nx.Graph()
# construct the original graph
for i in range(0, len(states) - 1):
G.add_edge(hash(states[i]), hash(states[i + 1]), name=moves[i])
# two steps of shortest path finding is enough
for _ in range(2):
# add all possible states with a given depth
for i in range(self.depth):
G = self._update_G(G)
shortest_path = nx.shortest_path(G, source=hash(state), target=hash(solution_state))
G = self._remove_nodes(G, shortest_path)
gc.collect()
moves = self._get_final_moves(shortest_path, G)
return [self.state_hash_dict[x] for x in shortest_path], moves
def _update_G(self, G: nx.Graph) -> nx.Graph:
# add all possible states for each node
nodes = []
for move in self.handler.allowed_moves:
for node in G.nodes:
state = self.handler.apply_move(self.state_hash_dict[node], move)
hash_state = hash(state)
self.state_hash_dict[hash_state] = state
nodes.append([node, hash_state, move])
for u, v, move in nodes:
G.add_edge(u, v, name=move)
return G
def _remove_nodes(self, G: nx.Graph, shortest_path: list[int]) -> nx.Graph:
# clean up the graph
nodes_to_remove = []
for node in G.nodes:
if node not in shortest_path:
nodes_to_remove.append(node)
G.remove_nodes_from(nodes_to_remove)
return G
def _get_final_moves(self, path: list[int], G: nx.Graph) -> list[str]:
# take the shortest path and check the moves
moves = []
for i in range(0, len(path) - 1):
hash_state_1, hash_state_2 = path[i], path[i+1]
state_1 = self.state_hash_dict[hash_state_1]
state_2 = self.state_hash_dict[hash_state_2]
move = G.get_edge_data(hash_state_1, hash_state_2)['name']
# graph edges are not bidirectional but some moves can be symmetrical
state_moved = self.handler.apply_move(state_1, move)
if state_moved == state_2:
moves.append(move)
continue
move = self._reverse_move(move)
state_moved = self.handler.apply_move(state_1, move)
if state_moved == state_2:
moves.append(move)
continue
return moves
def _reverse_move(self, move: str) -> str:
# actual only for globes
if move[0] == 'f':
return move
if move[0] == '-':
return move[1:]
return '-' + move
import numpy as np
import json
class GlobeHandler:
def __init__(self, globe_type: str, allowed_moves: str):
self.shape = self.extract_shape(globe_type)
self.moves_dict = json.loads(allowed_moves.replace("\'", "\""))
self.allowed_moves = self.get_allowed_moves(self.moves_dict)
def extract_shape(self, globe_type: str) -> tuple[int]:
a, b = globe_type[6:].split('/')
return int(a) + 1, int(b) * 2
def get_allowed_moves(self, moves_dict: dict) -> list[str]:
allowed_moves = []
for move in moves_dict.keys():
allowed_moves.append(move)
if move[0] == 'r':
allowed_moves.append('-' + move)
return allowed_moves
def apply_move(self, state: str, move: str) -> str:
arr = state.split(';')
if move[0] == '-' and move[1] == 'f':
move = move[1:]
if move[0] != '-':
result_arr = []
for i in self.moves_dict[move]:
result_arr.append(arr[i])
return ';'.join(result_arr)
result_arr = np.asarray(arr).reshape(self.shape)
result_arr = self._apply_minus_r_move(result_arr, move)
return ';'.join(result_arr.reshape(1, -1)[0])
def _apply_minus_r_move(self, arr: np.ndarray, move: str) -> np.ndarray:
idx = int(move[2:])
arr[idx] = np.append(arr[idx][-1], arr[idx][:-1])
return arrI hope this short note can help someone, good luck!
