[Using LSH Algorithm for Document Search]
Locality sensitive hashing for the document searching
In this article, I will propose and analyze an improved LSH algorithm for the text retrieval problem. First of all, I recommend studying several articles about LSH itself (this one, for example), because I will not delve into the mathematics of this algorithm.
If you are already familiar with the algorithm, here is a short reminder of its features:
- The algorithm approximates the Jaccard metric, but does so faster with minimal loss of accuracy.
- This is a powerful algorithm that can improve search performance. It can be used directly as a document search tool or as part of a recommendation system that can find relevant documents (due to the nature of the algorithm, relevance here coincides with syntactic similarity).
- Articles about the algorithm use specific terms:
- The shingle is a fragment of the original document. When we talk about textual similarity, a shingle in most cases is a classic character n-
gram. But I have also used LSH with n-gram tokens for specific tasks. Shingling is then a tokenization process.
- Min Hashing is a vectorization process that converts the original set of shingles into a signature.
- LSH converts signatures into buckets by splitting them into bands and adding strings with the same bands together. This allows us to aggregate similar strings faster.
from typing import List, Tuple, Dict, Set
import pandas as pd
import re
import numpy as np
from collections import Counter, defaultdict
import pickle
import random
import hashlib
from tqdm.auto import tqdm
from datetime import datetime
import seaborn as sns
import matplotlib.pyplot as plt1. Straight approach
Before we get into LSH itself, I'd like to directly measure the key metrics to understand what we're getting into. I use the Google trends corpus because it contains short queries that are easy to work with. Below I will do some pre-processing.
def get_ngrams(s: str, ngram_range: int = 2) -> Set[str]:
result = set()
for i in range(ngram_range, len(s) + 1):
result.add(s[i - ngram_range: i])
return result
def jaccard_score(s1: Set[str], s2: Set[str]) -> float:
return len(s1.intersection(s2)) / len(s1.union(s2))df = pd.read_csv('data/trends.csv')
df
location year category rank query
0 Global 2001 Consumer Brands 1 Nokia
1 Global 2001 Consumer Brands 2 Sony
2 Global 2001 Consumer Brands 3 BMW
3 Global 2001 Consumer Brands 4 Palm
4 Global 2001 Consumer Brands 5 Adobe
... ... ... ... ... ...
26950 Vietnam 2020 Là Gì? 1 Virus Corona là gì
26951 Vietnam 2020 Là Gì? 2 Miễn thị thực là gì
26952 Vietnam 2020 Là Gì? 3 Đầu cắt moi là gì
26953 Vietnam 2020 Là Gì? 4 Bệnh bạch hầu là gì
26954 Vietnam 2020 Là Gì? 5 Đông Lào là gì
[26955 rows x 5 columns]df['query'] = df['query'].apply(lambda x: x.lower())
corpus = df[df['query'].apply(lambda x: re.findall('[^a-z0-9]', x) == [])]['query'].unique()
len(corpus)
# 2254corpus[:5]
# array(['nokia', 'sony', 'bmw', 'palm', 'adobe'], dtype=object)I will solve the problem of finding the top 3 most similar queries. Important note - I will be running all processes in one thread. With the classic approach, I need to calculate the Jaccard metrics between the example and each query in the corpus. To speed up this process, I will save the corpus n-grams into a simple dictionary in advance. To measure the speed of the direct approach, I scan the entire corpus and calculate Jaccard metrics for each example. And to get the maximum Jaccard score we can achieve, I calculate the Jaccard score between the most similar pairs and average it.
%%time
ngram_dict = {}
corpus_ngrams = {}
for word in corpus:
ngrams = get_ngrams(word)
corpus_ngrams[word] = ngrams
for ngram in ngrams:
k = len(ngram_dict)
if ngram not in ngram_dict:
ngram_dict[ngram] = k
# CPU times: user 2.66 s, sys: 31.9 ms, total: 2.69 s
# Wall time: 2.69 s%%time
jaccard_matrix = np.zeros((len(corpus), len(corpus)))
for i, left_ngrams in enumerate(corpus_ngrams.values()):
for j in range(i + 1, len(corpus)):
right_ngrams = corpus_ngrams[corpus[j]]
jaccard_matrix[i, j] = jaccard_score(left_ngrams, right_ngrams)
jaccard_matrix += jaccard_matrix.T
# CPU times: user 2.66 s, sys: 31.9 ms, total: 2.69 s
# Wall time: 2.69 sThe algorithm training time took approximately 2-3 seconds (Macbook Pro 2,6 GHz 6-Core Intel Core i7). Let's make sure we've counted the nearest pairs correctly.
np.argmax(jaccard_matrix, axis=0)
# array([ 855, 1782, 1247, ..., 37, 424, 221])print(corpus[0], corpus[855])
print(corpus[1], corpus[1782])
print(corpus[-1], corpus[221])
# nokia snooki
# sony sona
# viettelstudy amstettenLet's calculate the maximum average score we can get close to.
jaccard_matrix.max(axis=0).mean()
# 0.40955150883139924def base_corpus_running():
for s in corpus:
left_ngrams = get_ngrams(s)
if len(left_ngrams) < 2:
continue
scores = []
for right_ngrams in corpus_ngrams.values():
scores.append(jaccard_score(left_ngrams, right_ngrams))
_ = corpus[np.argsort(scores)[::-1][:3]]
returnAnd let's calculate the time spent searching for the nearest strings in the entire corpus.
%%time
base_corpus_running()
# CPU times: user 3.98 s, sys: 8.3 ms, total: 3.99 s
# Wall time: 3.99 sThe direct approach has obvious problems: storing n-grams requires a lot of memory (storing one-hot encoded vectors is no longer efficient), it does not scale well, and it is a slow algorithm. Of course, we wouldn't do this in real life, but these metrics clearly show the starting position.
2. Classic LSH
But how does classic LSH work? The first step is shingling. As I mentioned, this is the same process as converting tokens to n-grams. The next step is to get a one-hot vector of shingles. But before this, it is necessary to calculate all possible shingles of the corpus.
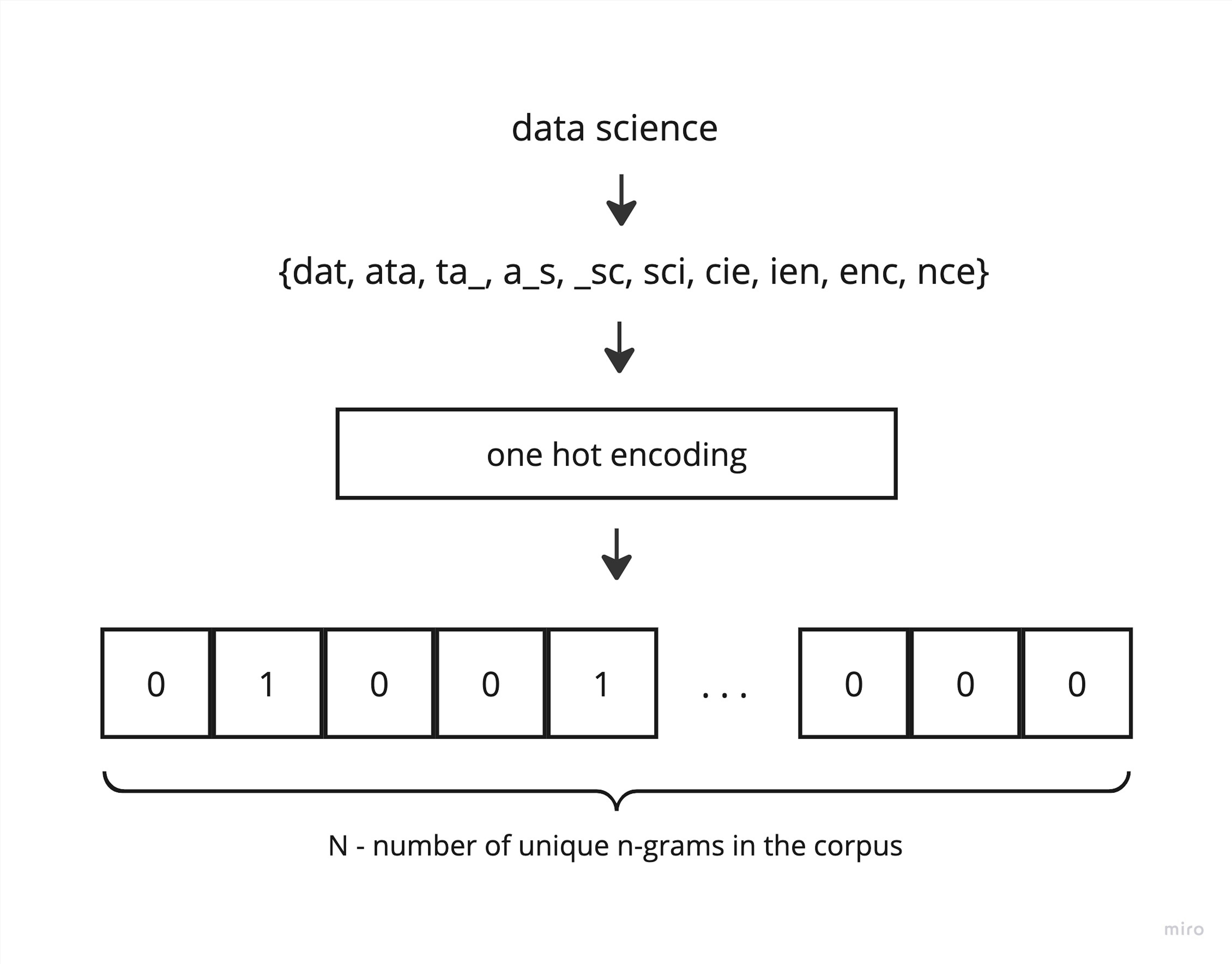
The main trick of LSH is to approximate an one hot vector by iteratively applying min hashing functions. Here is an example of such a function: this is a vector of permutation indices. We can sort the original vector by this permuted vector, and then the minimum hash value is the index of the first occurrence of 1 in the permuted vector. A signature is a combination of the minimum hash values that we obtain after applying several permutations to the original vector.
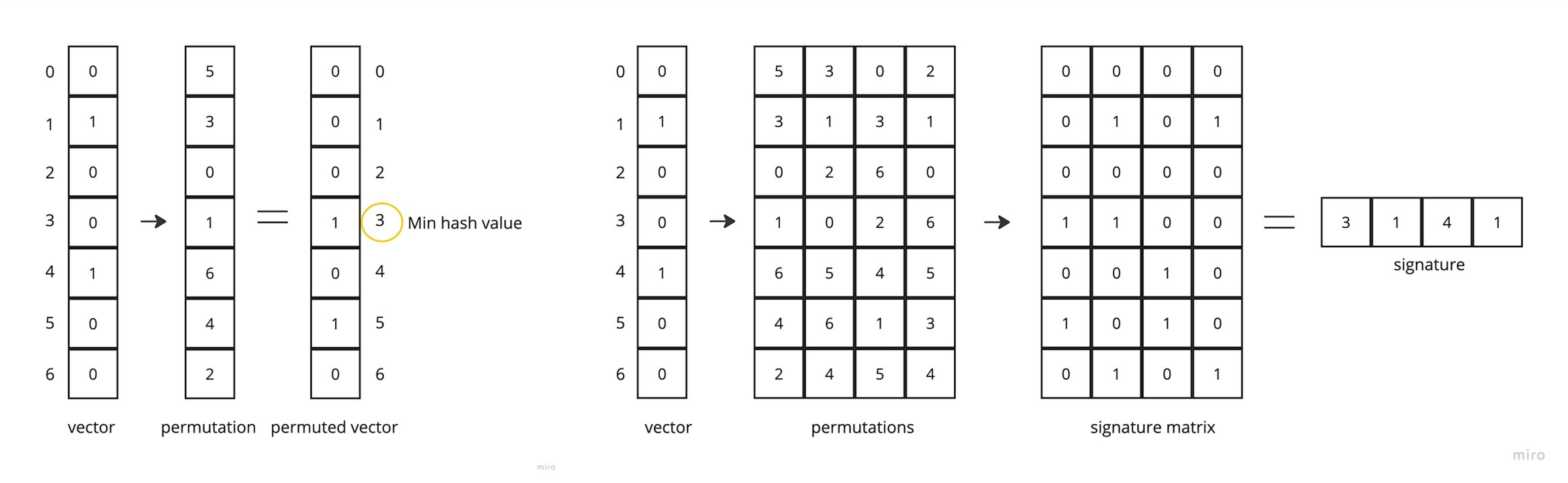
These permutations must be configured once after we have all possible shingles, and cannot be changed. Here we can notice the drawback of such an algorithm - if we want to add new documents with new shingles to the corpus, we need to update all the permutations and at the output we will get different vectors (signatures). It's not a big deal, the algorithm still works, but the metrics may change.
After receiving signatures, we need to create buckets. Here we will use another trick to improve the efficiency of the algorithm and speed it up. We split our signature into bands of the selected length, obtaining rows, and use them as bucket keys. We use the indices of the corresponding source strings in the corpus as the value. As a result, we get similar strings (strings with the same bands) in one bucket. Of course, strings in different buckets partially overlap each other, and to find the most similar candidates, we can simply count the number of overlapping bands.
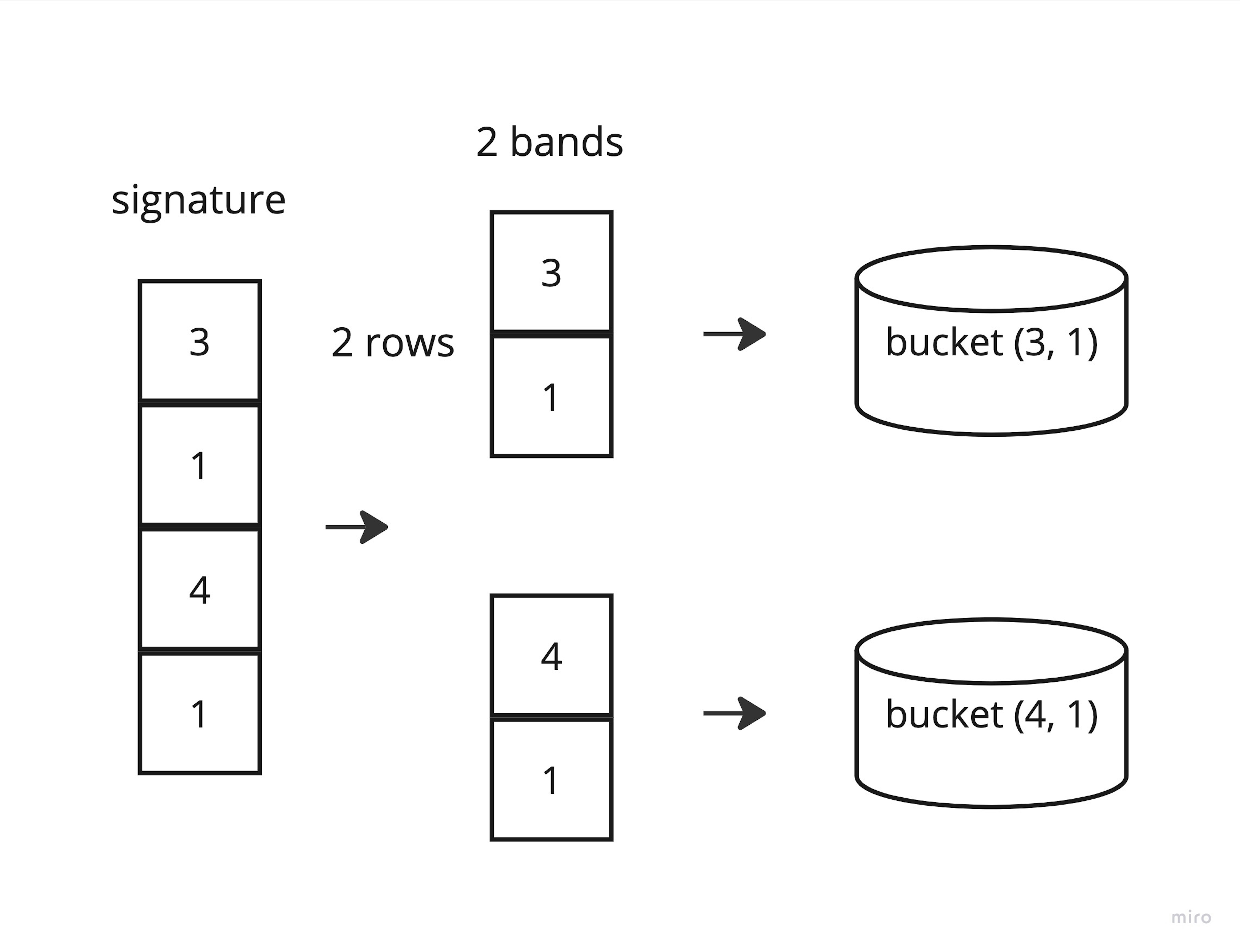
Classic LSH code
class LSHSearcher:
"""Local Sensitive Hashing algorithm.
Args:
k: int - shingle size.
size: int - number of hash funcs (vector size).
n_bands: int - number of bands to split signatures.
n_rows: int - band size. n_bands * n_rows must be equal to size.
"""
def __init__(
self,
k: int = 3,
size: int = 20,
n_bands: int = 10,
n_rows: int = 2,
):
assert n_bands * n_rows == size, 'Incompatible parameters'
self.k = k
self.size = size
self.n_bands = n_bands
self.n_rows = n_rows
def fit(self, corpus: List[str]) -> None:
"""Train model. Form buckets"""
corpus = list(corpus)
self.vocab_ = corpus
self.shingle_dict, corpus_shingles = self._fit_shingle_dict(corpus)
self.vector_size = len(self.shingle_dict)
self.hash_funcs_ = self._create_hash_funcs(self.size, self.vector_size)
signatures = [self._get_signature(row) for row in corpus_shingles]
X = np.asarray(signatures).T
self._fit_buckets(X)
def get_relevant_documents(
self,
query: str,
n_candidates: int = 3
) -> List[Tuple[str, int]]:
"""Search for the most relevant documents.
Args:
query: str
n_candidates: int - number of the returned documents.
Returns:
List[Tuple[str, int]] - list of documents and scores (number of overlapped bands).
"""
candidates = Counter()
X = self._transform([query])
X_bands = np.array_split(X, self.n_bands, axis=0)
for i, band in enumerate(X_bands):
band_id = tuple(list(band[:, 0]) + [str(i)])
candidates.update(list(self.hashbuckets_[band_id]))
return [(self.vocab_[x[0]], x[1]) for x in candidates.most_common(n_candidates)]
def _create_hash_funcs(self, size: int, length: int) -> List[np.ndarray]:
funcs = []
indices = np.arange(0, length, 1)
for _ in range(size):
arr = indices.copy()
np.random.shuffle(arr)
funcs.append(arr)
return funcs
def _fit_shingle_dict(self, corpus: List[str]) -> Tuple[Dict[str, int], List[Set[str]]]:
shingle_dict = {}
corpus_shingles = []
for row in corpus:
shingles = self._get_shingles(row)
corpus_shingles.append(shingles)
for shingle in shingles:
k = len(shingle_dict)
if shingle not in shingle_dict:
shingle_dict[shingle] = k
return shingle_dict, corpus_shingles
def _transform(self, corpus: List[str]) -> np.ndarray:
signatures = [self._get_signature(self._get_shingles(row)) for row in corpus]
return np.asarray(signatures).T
def _get_shingles(self, row: str) -> List[str]:
shingles = set()
for i in range(self.k, len(row) + 1):
shingles.add(row[i-self.k: i])
return list(shingles)
def _get_signature(self, shingles_row: List[str]) -> List[int]:
# one hot encoding
vector = np.zeros(self.vector_size)
for shingle in shingles_row:
if shingle not in self.shingle_dict:
continue
vector[self.shingle_dict[shingle]] = 1
# min hashing
signature = []
for hash_func in self.hash_funcs_:
min_value = self._apply_hash_func(vector, hash_func)
signature.append(min_value)
return signature
def _apply_hash_func(self, vector: np.ndarray, func: List[int]) -> int:
for i, val in enumerate(func):
if vector[val] == 1:
return i
return i
def _fit_buckets(self, X: np.ndarray) -> None:
_, d = X.shape
self.hashbuckets_ = defaultdict(set)
bands = np.array_split(X, self.n_bands, axis=0)
for i, band in enumerate(bands):
for j in range(d):
band_id = tuple(list(band[:, j]) + [str(i)])
self.hashbuckets_[band_id].add(j)
def save(self, filepath: str) -> None:
with open(filepath, 'wb') as f:
pickle.dump(self, f)
@staticmethod
def load(filepath: str) -> None:
with open(filepath, 'rb') as f:
return pickle.load(f)Here below are some calculations in which I measure speed and quality indicators depending on different numbers of bands and rows. Obviously we get the maximum Jaccard score when row length is 1 (when we split the signature at each value) and when we choose a large signature vector size, but this may not be efficient on a large corpus, so we should look for a speed-quality trade-off.
Auxiliary calculation functions
def get_searcher_scores(searcher: LSHSearcher) -> float:
searcher_scores = []
for word, ngrams in corpus_ngrams.items():
candidates = searcher.get_relevant_documents(word)
if len(candidates) > 1:
candidate = candidates[1][0]
searcher_scores.append(jaccard_score(ngrams, corpus_ngrams[candidate]))
else:
searcher_scores.append(0)
return np.mean(searcher_scores)
def experiments_running() -> None:
BANDS = [5, 10, 20, 30, 50]
ROWS = [5, 4, 3, 2, 1]
searcher_scores = np.zeros((len(BANDS), len(ROWS)))
training_time = np.zeros((len(BANDS), len(ROWS)))
for i, n_bands in tqdm(enumerate(BANDS), total=len(BANDS)):
for j, n_rows in enumerate(ROWS):
start_time = datetime.now()
searcher = LSHSearcher(k=2, size=n_bands*n_rows, n_bands=n_bands, n_rows=n_rows)
searcher.fit(corpus)
training_time[i, j] = (datetime.now() - start_time).seconds
searcher_scores[i, j] = get_searcher_scores(searcher)
fig, (ax1, ax2) = plt.subplots(figsize=(15, 7), nrows=1, ncols=2)
sns.heatmap(
searcher_scores,
annot=True, cbar=False,
xticklabels=BANDS,
yticklabels=ROWS,
ax=ax1
)
ax1.set(xlabel="Bands", ylabel="Rows", title="Jaccard scores")
sns.heatmap(
training_time,
annot=True, cbar=False,
xticklabels=BANDS,
yticklabels=ROWS,
)
ax2.set(xlabel="Bands", title="Algorithm training time, sec")
plt.show()
return
def corpus_running(searcher: LSHSearcher) -> None:
_ = [searcher.get_relevant_documents(s) for s in corpus]
return
experiments_running()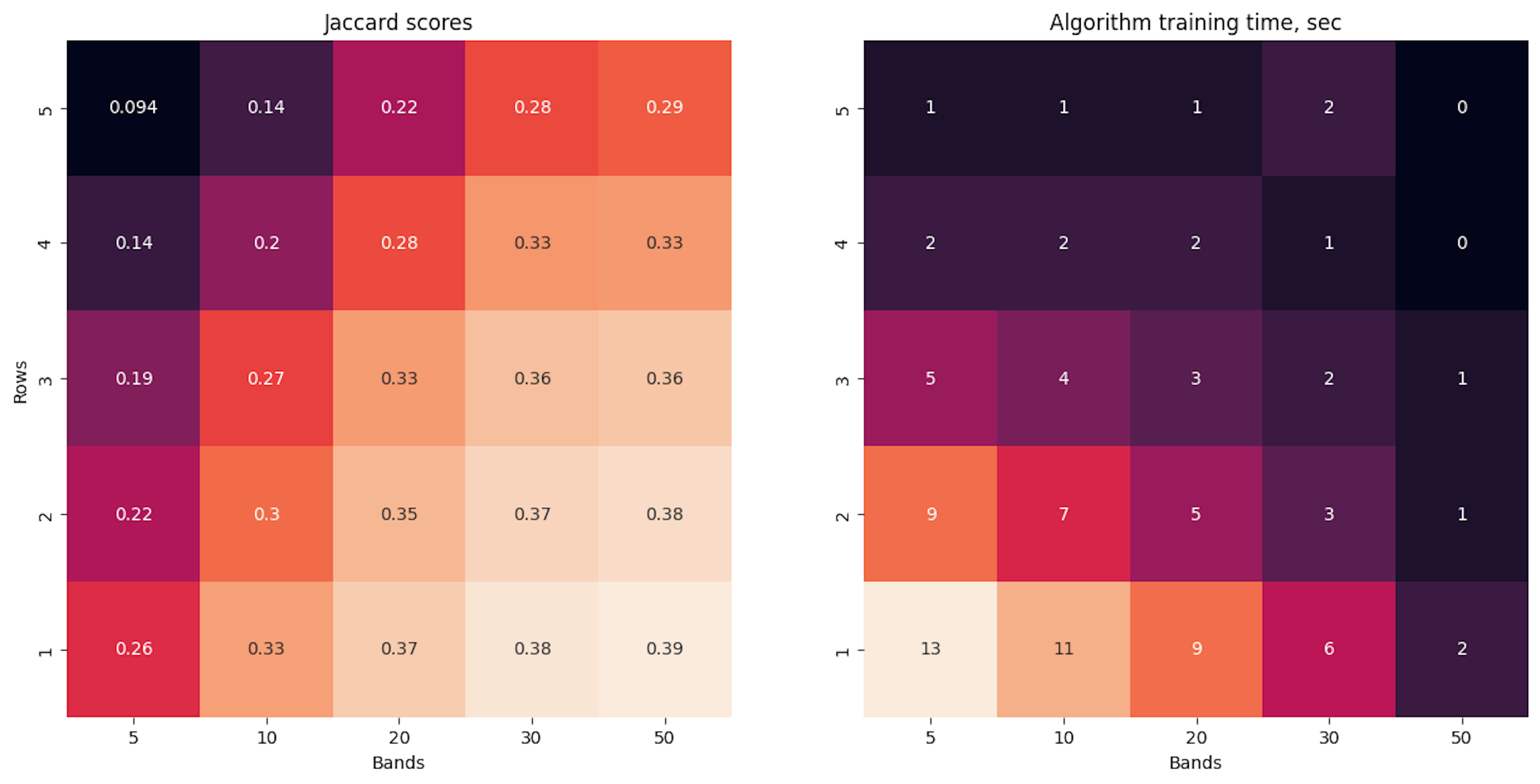
%%time
lsh = LSHSearcher(k=2, size=50, n_bands=50, n_rows=1)
lsh.fit(corpus)
# CPU times: user 4.34 s, sys: 25.2 ms, total: 4.37 s
# Wall time: 4.4 slsh.get_relevant_documents('nokia')
# [('nokia', 50), ('kia', 26), ('snooki', 23)]%%time
corpus_running(lsh)
# CPU times: user 4.9 s, sys: 29.1 ms, total: 4.93 s
# Wall time: 4.93 sIn the current example, we get the maximum score when n_rows = 1 and n_bands = 50. And the processing speed of such an algorithm is even more as with the direct approach. But on a large corpus, I believe we will get a significant improvement.
3. Advanced LSH
So, in the advanced version of the algorithm, I propose to do the same thing, but eliminate the inefficient one-hot encoding. First of all, I replace it by hashing the strings into an integer. We can use Python's built-in hash function. This is very fast, but then we won't be able to save and reuse the algorithm even after fixing all the seeds, so md5 hashing is an equivalent replacement.
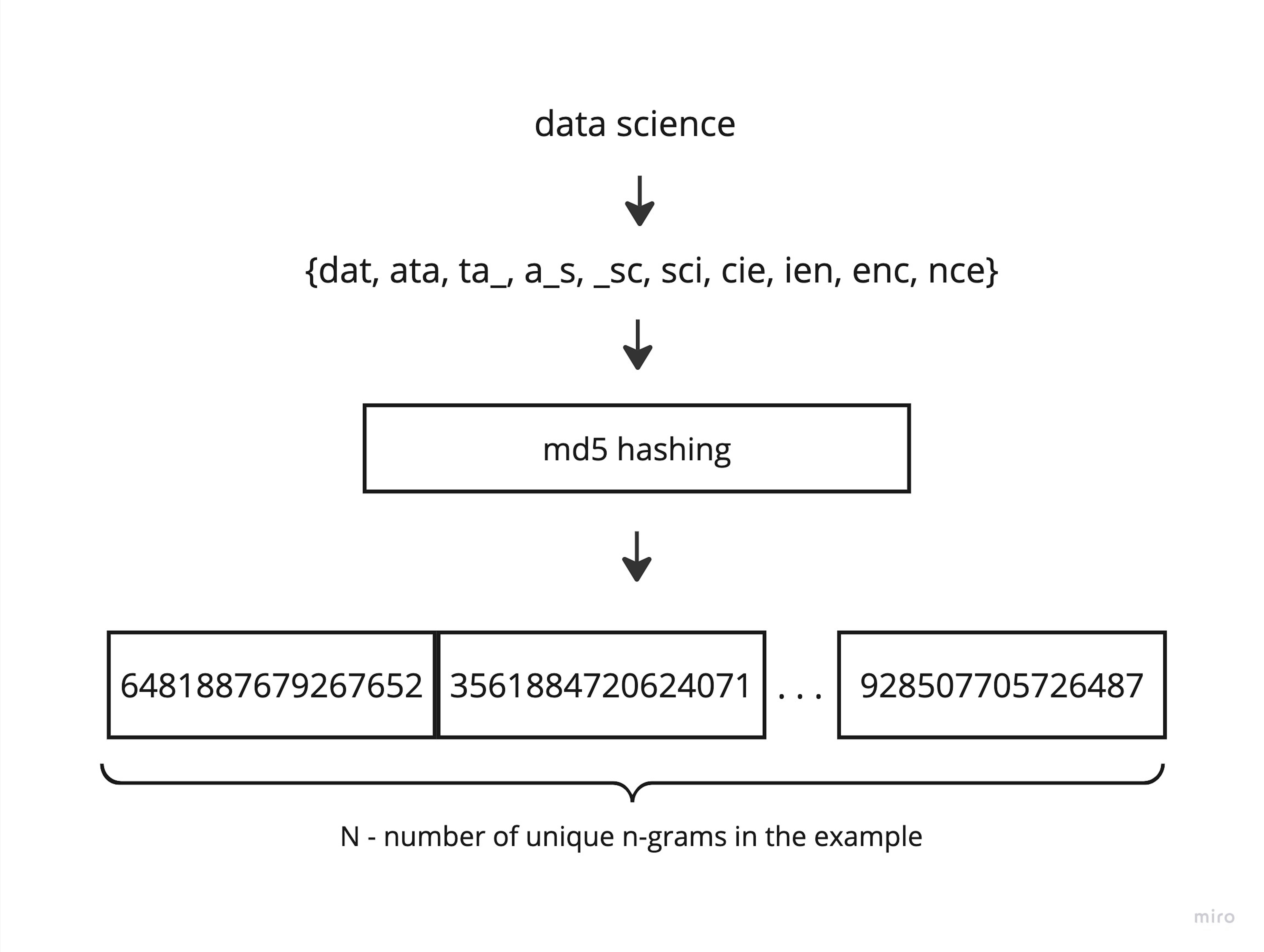
And the next step is also hashing (don't confuse them). To get the minimum hash value, we pick a random integer, raise each shingle's hash value to that power, find the remainder of division by any selected large prime number, and then simply find the minimum value of that vector. To obtain a signature, we only need to prepare a set of random integers and perform the same operations sequentially.
The remaining steps are completely similar.
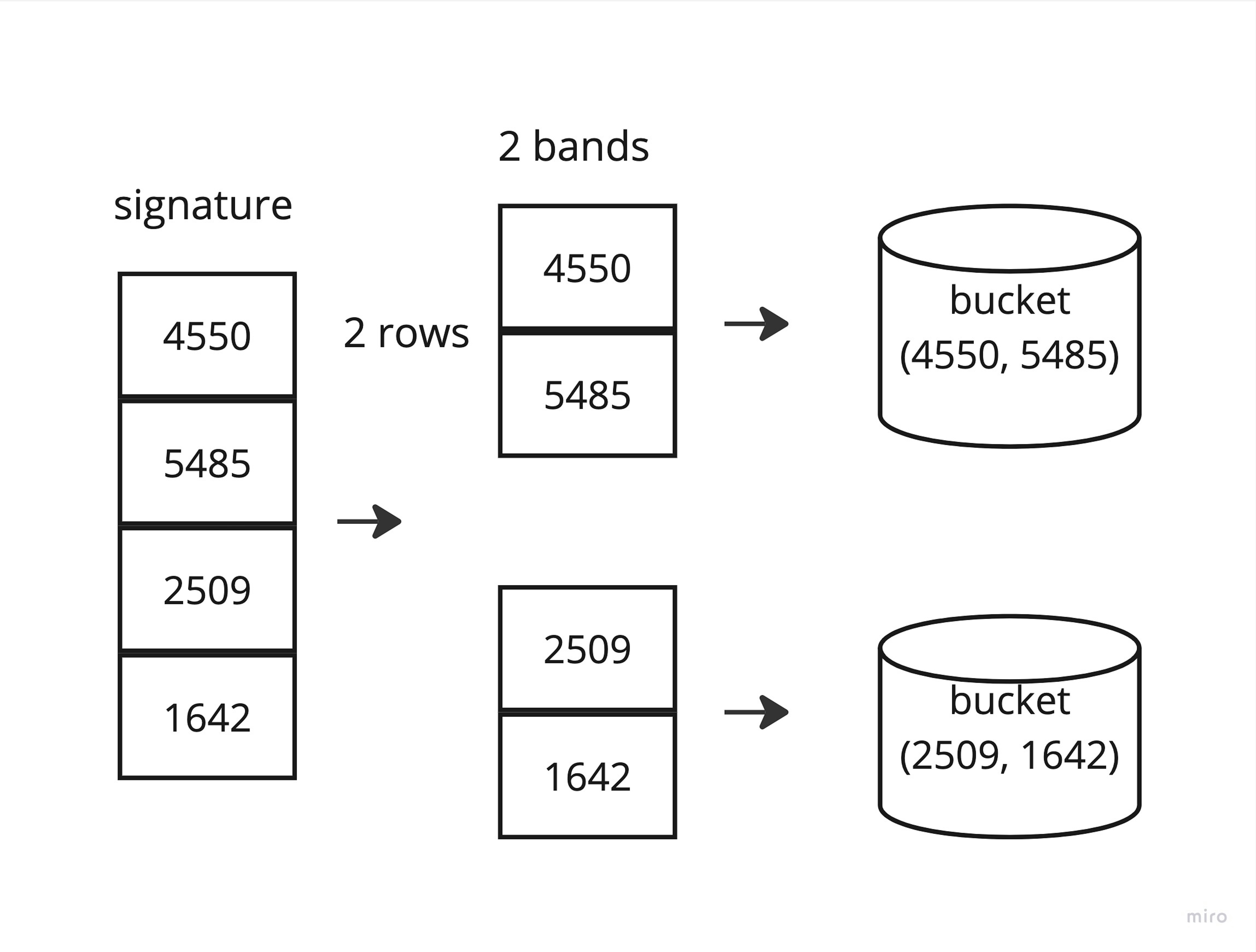
The advantage of this version is the processing speed. We don't store large one-hot permutations, don't waste time sorting by permutations, but simply hash strings into integers and perform simple math operations. Obviously, we can update the corpus at any time because we don't have to recalculate the hash functions.
Advanced LSH Code
class LSHSearcher:
"""Local Sensitive Hashing algorithm.
Args:
k: int - shingle size.
size: int - number of hash funcs (vector size).
n_bands: int - number of bands to split signatures.
n_rows: int - band size. n_bands * n_rows must be equal to size.
"""
def __init__(
self,
k: int = 3,
size: int = 20,
n_bands: int = 10,
n_rows: int = 2,
):
assert n_bands * n_rows == size, 'Incompatible parameters'
self.k = k
self.size = size
self.n_bands = n_bands
self.n_rows = n_rows
def fit(self, corpus: List[str]) -> None:
"""Train model. Form buckets"""
corpus = list(corpus)
self.vocab_ = corpus
self.hash_funcs_ = self._create_hash_funcs(self.size)
X = self._transform(corpus)
self._fit_buckets(X)
def get_relevant_documents(
self,
query: str,
n_candidates: int = 3
) -> List[Tuple[str, int]]:
"""Search for the most relevant documents.
Args:
query: str
n_candidates: int - number of the returned documents.
Returns:
List[Tuple[str, int]] - list of documents and scores (number of overlapped bands).
"""
candidates = Counter()
X = self._transform([query])
X_bands = np.array_split(X, self.n_bands, axis=0)
for i, band in enumerate(X_bands):
band_id = tuple(list(band[:, 0]) + [str(i)])
candidates.update(list(self.hashbuckets_[band_id]))
return [(self.vocab_[x[0]], x[1]) for x in candidates.most_common(n_candidates)]
def _create_hash_funcs(self, size: int) -> List[int]:
return [random.randint(0, 2**32) for _ in range(size)]
def _transform(self, corpus: List[str]) -> np.ndarray:
signatures = [self._get_signature(self._get_hash_shingles(row)) for row in corpus]
return np.asarray(signatures).T
def _get_hash_shingles(self, row: str) -> List[int]:
shingles = set()
for shingle in self._get_shingles(row):
shingles.add(self._get_hash(shingle))
return list(shingles)
def _get_shingles(self, row: str) -> str:
for i in range(self.k, len(row) + 1):
yield row[i-self.k: i]
def _get_hash(self, shingle: str) -> int:
md5 = hashlib.md5(shingle.encode())
return int(md5.hexdigest(), 16) % (10**16)
def _get_signature(self, shingles_row: List[int]) -> List[int]:
signature = [None for _ in range(self.size)]
for shingle_hash in shingles_row:
for i, hash_func in enumerate(self.hash_funcs_):
hash_value = self._apply_hash_func(shingle_hash, hash_func)
if not signature[i]:
signature[i] = hash_value
continue
signature[i] = min(signature[i], hash_value)
return signature
def _apply_hash_func(self, shingle_hash: int, hash_func: int) -> int:
return (shingle_hash ^ hash_func) % 17321
def _fit_buckets(self, X: np.ndarray) -> None:
_, d = X.shape
self.hashbuckets_ = defaultdict(set)
bands = np.array_split(X, self.n_bands, axis=0)
for i, band in enumerate(bands):
for j in range(d):
band_id = tuple(list(band[:, j]) + [str(i)])
self.hashbuckets_[band_id].add(j)
def save(self, filepath: str) -> None:
with open(filepath, 'wb') as f:
pickle.dump(self, f)
@staticmethod
def load(filepath: str) -> None:
with open(filepath, 'rb') as f:
return pickle.load(f)The measurements are the same here and we see that the quality is the same, but the training time is very low.
experiments_running()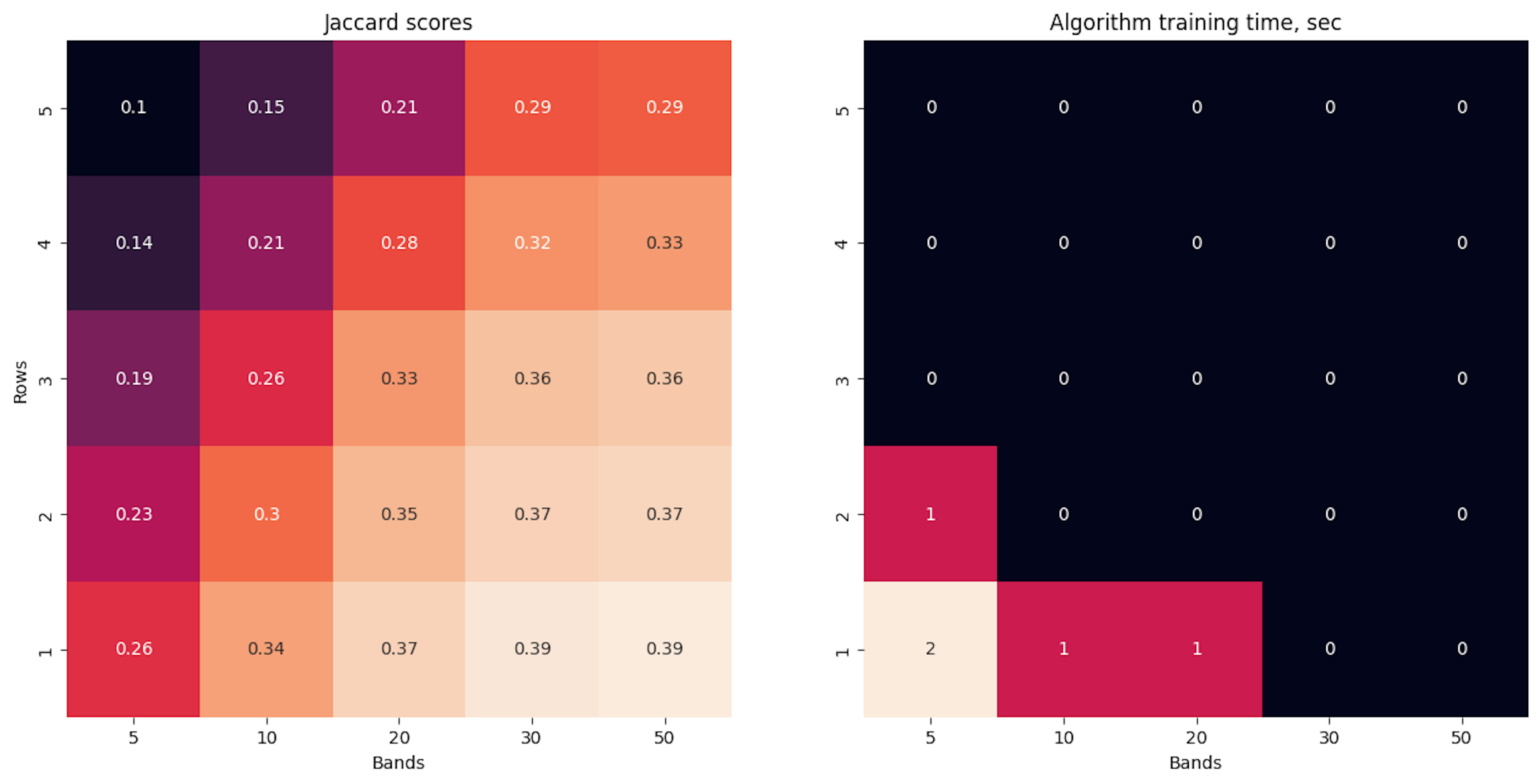
%%time
lsh = LSHSearcher(k=2, size=50, n_bands=50, n_rows=1)
lsh.fit(corpus)
# CPU times: user 419 ms, sys: 2.76 ms, total: 422 ms
# Wall time: 423 mslsh.get_relevant_documents('nokia')
# [('nokia', 50), ('nook', 24), ('snooki', 23)]%%time
corpus_running(lsh)
# CPU times: user 1.26 s, sys: 6.5 ms, total: 1.27 s
# Wall time: 1.27 sAnd the search is completed in an very short time.
In conclusion, I would like to note that such an algorithm can be extended to shingling n-grams of tokens. Thanks to the memory efficiency, we can not be afraid of the huge number of possible shingles. To do this, it is enough to make small changes to the string-to-integer hashing code:
def _get_hash(self, shingle: Tuple[str]) -> int:
md5 = hashlib.md5()
for element in shingle:
md5.update(element.encode())
return int(md5.hexdigest(), 16) % (10**16)And we must return tuples of strings when shingling to hash them.
def _get_shingles(self, row: Union[str, List[str]]) -> Tuple[str]:
for i in range(self.k, len(row) + 1):
yield tuple(row[i-self.k: i])The full code below. In practice, I used 1-gram tokens in a string matching problem and it was very efficient.
LSH with support for working with tokens
class LSHSearcher:
"""Local Sensitive Hashing algorithm.
Args:
kind: str - algorithm type (symbol or token)
k: int - shingle size.
size: int - number of hash funcs (vector size).
n_bands: int - number of bands to split signatures.
n_rows: int - band size. n_bands * n_rows must be equal to size.
"""
def __init__(
self,
kind: str = 'symbol',
k: int = 3,
size: int = 20,
n_bands: int = 10,
n_rows: int = 2,
):
assert n_bands * n_rows == size, 'Incompatible parameters'
self.kind = kind
self.k = k
self.size = size
self.n_bands = n_bands
self.n_rows = n_rows
def fit(self, corpus: List[str]) -> None:
"""Train model. Form buckets"""
corpus = list(corpus)
self.vocab_ = corpus
self.hash_funcs_ = self._create_hash_funcs(self.size)
X = self._transform(corpus)
self._fit_buckets(X)
def get_relevant_documents(
self,
query: str,
n_candidates: int = 3
) -> List[Tuple[str, int]]:
"""Search for the most relevant documents.
Args:
query: str.
n_candidates: int - number of the returned documents.
Returns:
List[Tuple[str, int]] - list of documents and scores (number of overlapped bands).
"""
candidates = Counter()
X = self._transform([query])
X_bands = np.array_split(X, self.n_bands, axis=0)
for i, band in enumerate(X_bands):
band_id = tuple(list(band[:, 0]) + [str(i)])
candidates.update(list(self.hashbuckets_[band_id]))
return [(self.vocab_[x[0]], x[1]) for x in candidates.most_common(n_candidates)]
def _create_hash_funcs(self, size: int) -> List[int]:
return [random.randint(0, 2**32) for _ in range(size)]
def _transform(self, corpus: List[str]) -> np.ndarray:
signatures = [self._get_signature(self._get_hash_shingles(self._tokenize(row))) for row in corpus]
return np.asarray(signatures).T
def _tokenize(self, row: str) -> Union[str, List[str]]:
if self.kind == 'symbol':
return row
return row.split()
def _get_hash_shingles(self, row: Union[str, List[str]]) -> List[int]:
shingles = set()
for shingle in self._get_shingles(row):
shingles.add(self._get_hash(shingle))
return list(shingles)
def _get_shingles(self, row: Union[str, List[str]]) -> Tuple[str]:
for i in range(self.k, len(row) + 1):
yield tuple(row[i-self.k: i])
def _get_hash(self, shingle: Tuple[str]) -> int:
md5 = hashlib.md5()
for element in shingle:
md5.update(element.encode())
return int(md5.hexdigest(), 16) % (10**16)
def _get_signature(self, shingles_row: List[int]) -> List[int]:
signature = [None for _ in range(self.size)]
for shingle_hash in shingles_row:
for i, hash_func in enumerate(self.hash_funcs_):
hash_value = self._apply_hash_func(shingle_hash, hash_func)
if not signature[i]:
signature[i] = hash_value
continue
signature[i] = min(signature[i], hash_value)
return signature
def _apply_hash_func(self, shingle_hash: int, hash_func: int) -> int:
return (shingle_hash ^ hash_func) % 17321
def _fit_buckets(self, X: np.ndarray) -> None:
_, d = X.shape
self.hashbuckets_ = defaultdict(set)
bands = np.array_split(X, self.n_bands, axis=0)
for i, band in enumerate(bands):
for j in range(d):
band_id = tuple(list(band[:, j]) + [str(i)])
self.hashbuckets_[band_id].add(j)
def save(self, filepath: str) -> None:
with open(filepath, 'wb') as f:
pickle.dump(self, f)
@staticmethod
def load(filepath: str) -> None:
with open(filepath, 'rb') as f:
return pickle.load(f)As a result, the advanced LSH has the same ability to approximate the Jaccard metric as the classic version of the algorithm. But there are no problems with scaling. The learning speed is higher (423 ms vs 4.4 s for the classic algorithm) and similar documents are found faster (1.27 s vs 4.93 s to run through the corpus completely).
